Su'S Blog

• 卷积与互相关计算
• 卷积
  • 动画演示
  • 二维卷积 torch.nn.Conv2d
  • 一维卷积 torch.nn.Conv1d
  • 三维卷积 torch.nn.Conv3d
• 反卷积（转置卷积）
  • 动画演示
  • 二维反卷积 torch.nn.ConvTranspose2d
  • 一维反卷积 torch.nn.ConvTranspose1d
  • 三维反卷积 torch.nn.ConvTranspose3d

代码：https://pytorch.org/docs/stable/_modules/torch/nn/modules/conv.html
官方文档：https://pytorch.org/docs/stable/nn.html#convolution-layers
动画演示：https://github.com/vdumoulin/conv_arithmetic

卷积与互相关计算

在深度学习领域，卷积定义为图像矩阵和卷积核的按位点乘，实质这种操作是互相关运算，而卷积需要把卷积核顺时针旋转180度然后再做点乘。

参见：https://en.wikipedia.org/wiki/Cross-correlation

在信号处理领域，互相关计算可以用来计算两个信号之间的相似性，也通过与已知信号比较用于寻找未知信号中的特性。

卷积

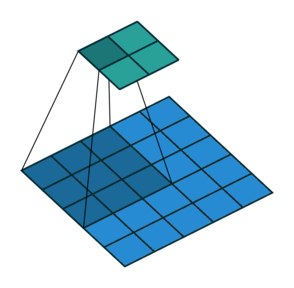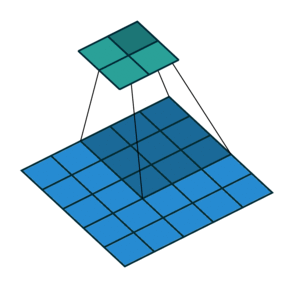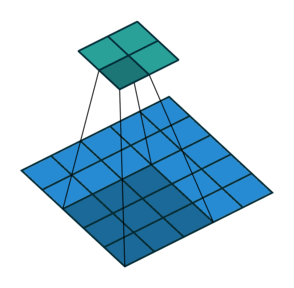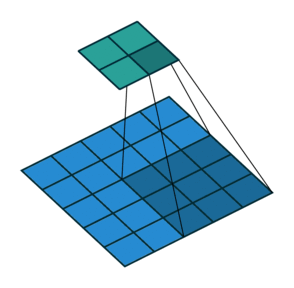
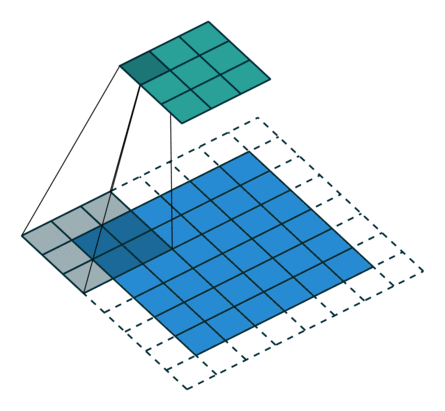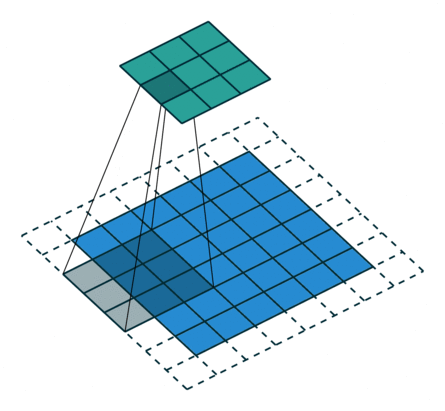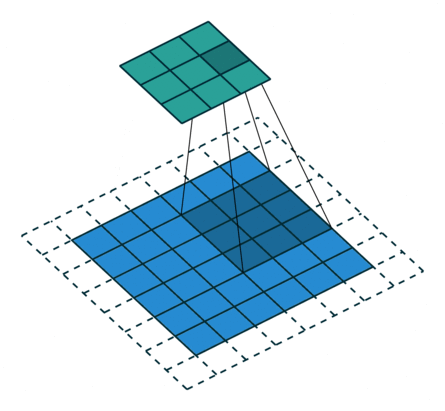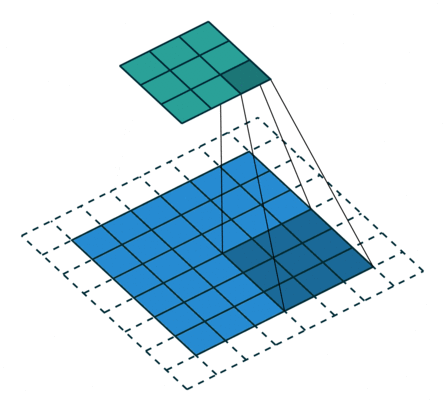
动画演示

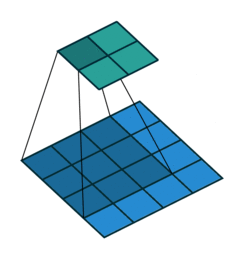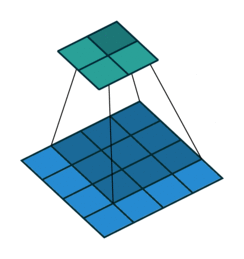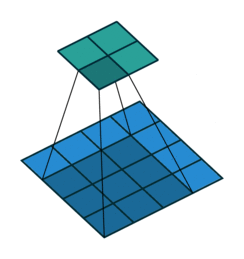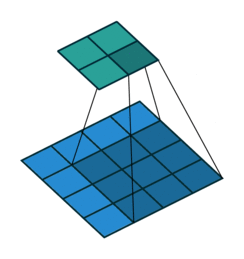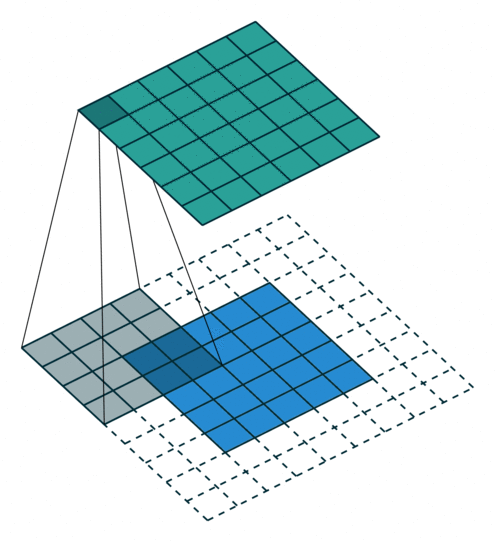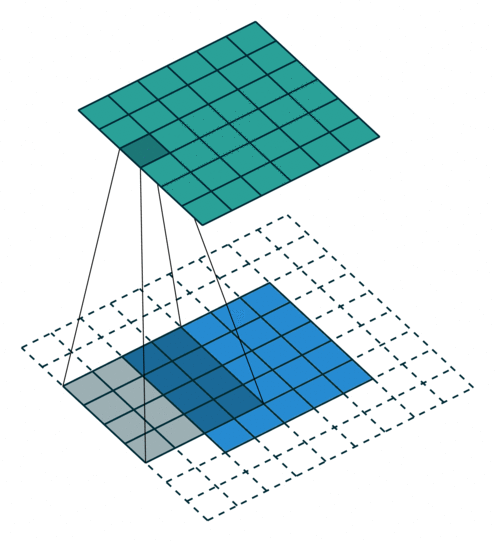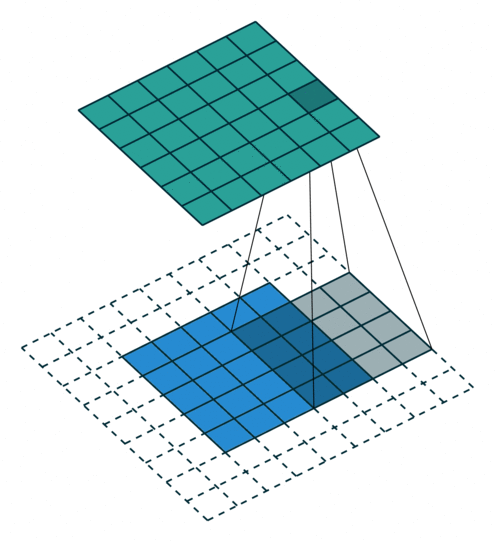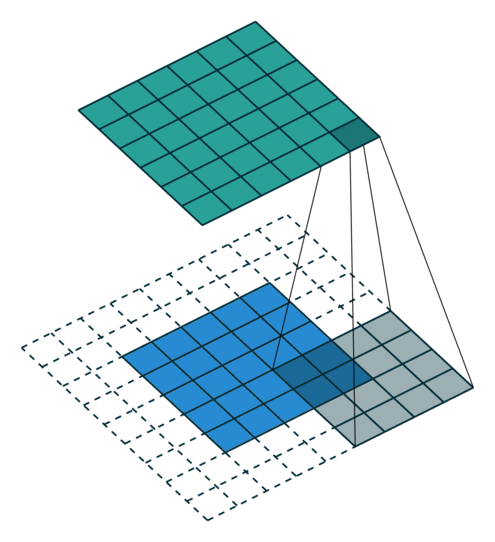No padding, no strides	Arbitrary padding, no strides
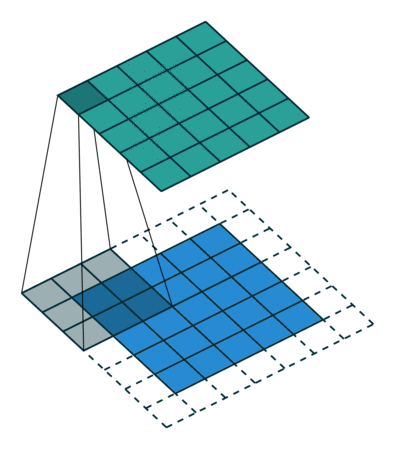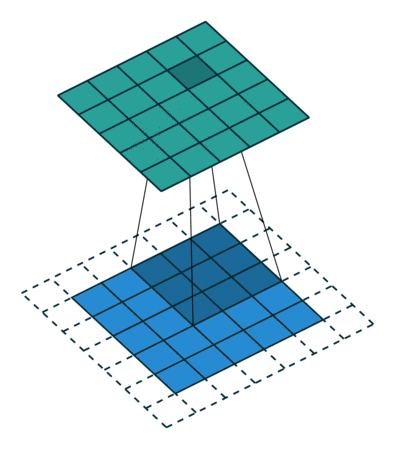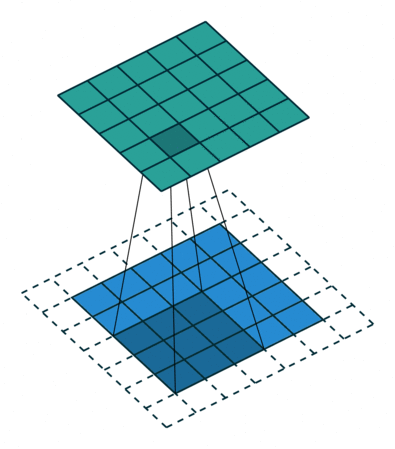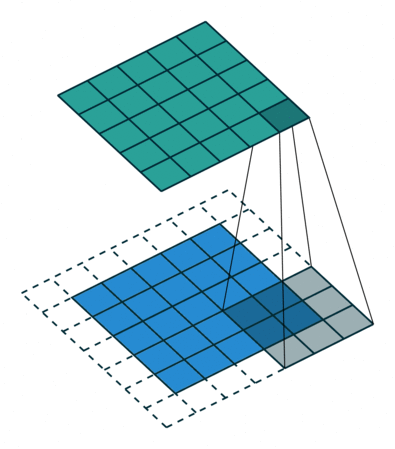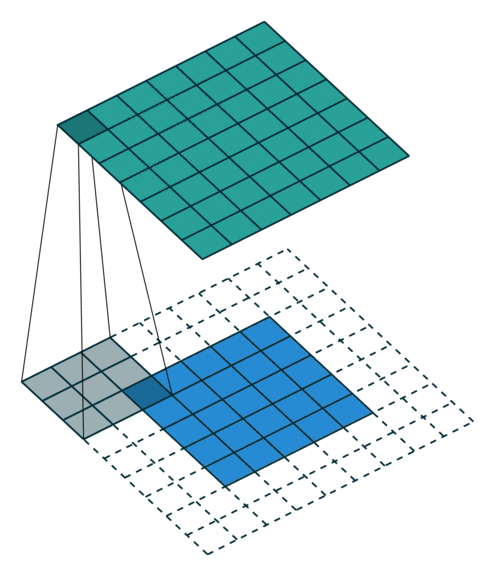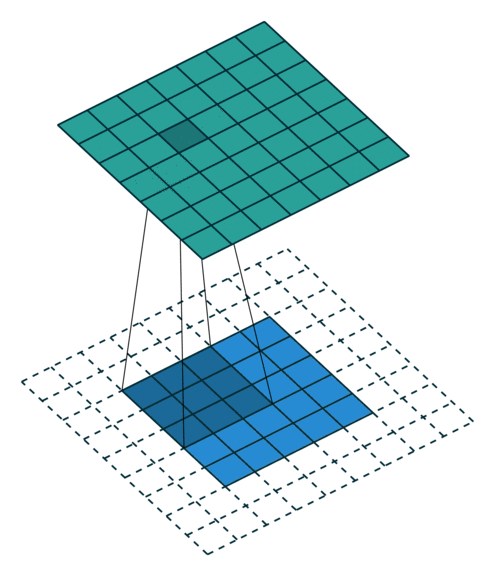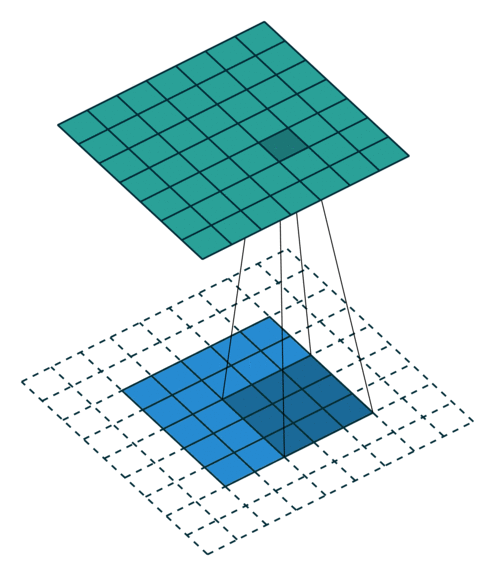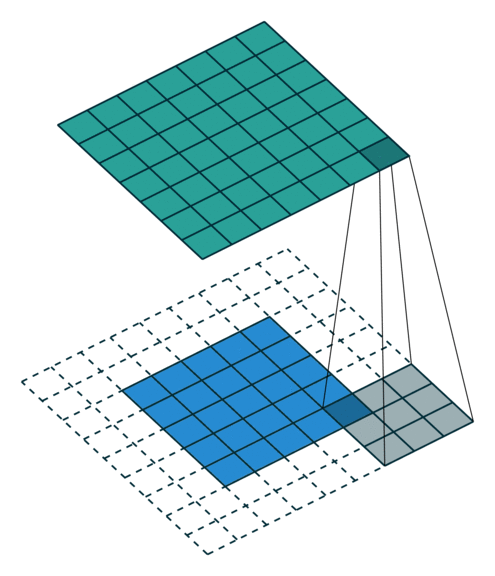Half padding, no strides	Full padding, no strides
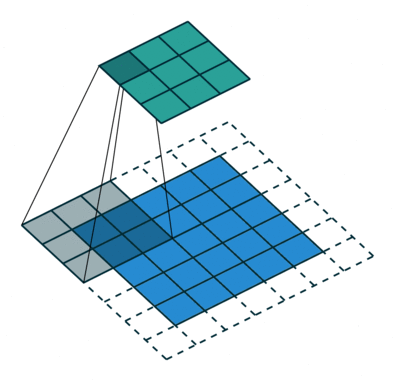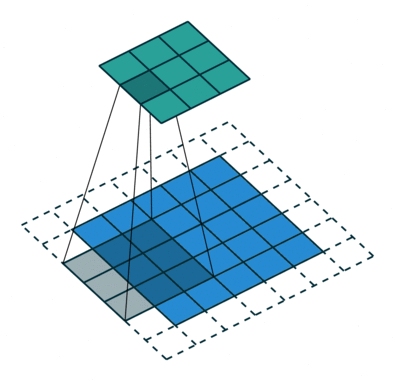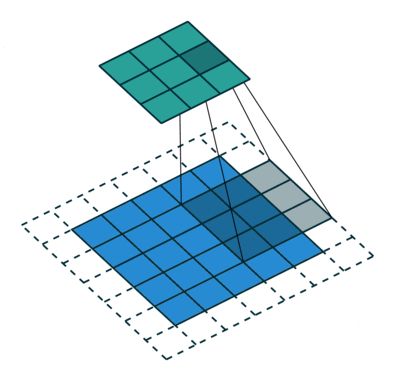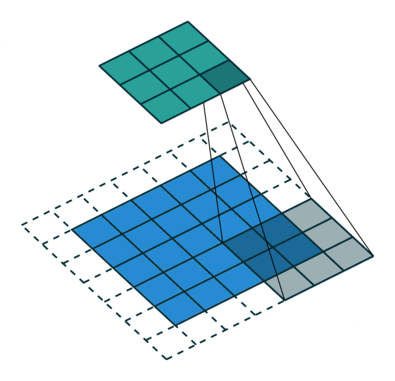No padding, strides	Padding, strides
Padding, strides (odd)

N.B.: Blue maps are inputs, and cyan maps are outputs.

二维卷积 torch.nn.Conv2d

class torch.nn.Conv2d (in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)

输入数据大小：$(N, C_{in}, H, W)$

输出数据大小：$(N, C_{out}, H_{out}, W_{out})$

2D 卷积的整个过程以下式表达：

其中 $\star$ 是 2D 互相关操作符, N 表示批（batch）的大小, C 表示通道数, H 输入数据的高（像素）, and W 表示数据的宽（像素）

其他参数

kernel_size (int or tuple) : 控制卷积核的大小。

stride (int or tuple, optional) ： 控制互相关的步长。

padding (int or tuple, optional) ： 控制两侧隐式零填充的数量，以填充每个维度的点数。

dilation (int or tuple, optional) ： 控制卷积核核点之间的间距。具体操作过程如下图所示，可以很好地显示扩张的作用

groups (int, optional) ： 控制输入和输出的连接。输入数据和输出数据的通道数必须同时被groups整除。例如：groups=1时，所有的输入卷积到所有的输出。groups=2时，有两个并列的卷积层，每个卷积层对应输入数据一半的通道数，同时也对应输出数据一半的通道数。groups= in_channels （输入数据的通道数）时 每个输入通道与对应的大小为 $\left\lfloor\frac{\text{out_channels}}{\text{in_channels}}\right\rfloor$ 的滤波器集合做卷积运算 。

深度卷积：当 groups == in_channels，out_channels == K * in_channels （其中K为正整数）时，被称为深度卷积。

输入数据大小：$(N, C_{in}, H_{in}, W_{in})$

输出数据大小：$(N, C_{out}, H_{out}, W_{out})$

其中：

一维卷积 torch.nn.Conv1d

class torch.nn.Conv1d (in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)

输入数据大小：$(N, C_{in}, L)$

输出数据大小： $(N, C_{out}, L_{out})$

1D 卷积的整个过程以下式表达：

其中 $\star$ 是 1D 互相关操作符, N 表示批（batch）的大小, C 表示通道数, L表示一维数据的长度。

多通道一维数据：
一维卷积常用于序列模型，自然语言处理领域。以声音为例，在同一维度上，不同的通道可以表示不同的音源的声音，通道1：人声，通道2：鼓声。即：不同的通道表示不同属性的一维序列数据。

关于一维卷积其余的属性和算法和下文中的二维卷积相似。

三维卷积 torch.nn.Conv3d

class torch.nn.Conv3d (in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)

相比于二维卷积，三维卷积的输入和输出是三维数据。输入数据的大小为：$(N, C_{in}, D, H, W)$，输出数据的大小为：$(N, C_{out}, D_{out}, H_{out}, W_{out})$

其余的概念和算法与二维卷积相同。

三维卷积的应用场景： 三维卷积常用于医学领域（CT影响），视频处理领域（检测动作及人物行为）

反卷积（转置卷积）

卷积操作的作用类似神经网络中的编码器，用于对高维数据进行低维特征提取，而 反卷积 通常用于将低维特征映射成高维输入，与卷积操作的作用相反。同时也是一种基于学习的上采样实现方法。

动画演示

No padding, no strides, transposed	Arbitrary padding, no strides, transposed
Half padding, no strides, transposed	Full padding, no strides, transposed
No padding, strides, transposed	Padding, strides, transposed
Padding, strides, transposed (odd)

N.B.: Blue maps are inputs, and cyan maps are outputs.

二维反卷积 torch.nn.ConvTranspose2d

class torch.nn.ConvTranspose2d (in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1)

反卷积和卷积在参数上的区别在于padding和output_padding。

padding ：控制0填充的大小。在输入数据的每个边隐式地添加 (kernel_size - 1 - padding) 个0。而在进行卷积操作时，需要填充的是(padding)个0。

output_padding Additional size added to one side of each dimension in the output shape

The padding argument effectively adds kernel_size - 1 - padding amount of zero padding to both sizes of the input. This is set so that when a Conv3d and a ConvTranspose3d are initialized with same parameters, they are inverses of each other in regard to the input and output shapes. However, when stride > 1, Conv3d maps multiple input shapes to the same output shape. output_padding is provided to resolve this ambiguity by effectively increasing the calculated output shape on one side. Note that output_padding is only used to find output shape, but does not actually add zero-padding to output.

输入数据大小：$(N, C_{in}, H_{in}, W_{in})$

输出数据大小：$(N, C_{out}, H_{out}, W_{out})$

其中：

一维反卷积 torch.nn.ConvTranspose1d

class torch.nn.ConvTranspose1d (in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1)

在计算方法和参数设置上与二维反卷积相似。

三维反卷积 torch.nn.ConvTranspose3d

class torch.nn.ConvTranspose3d (in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1)

在计算方法和参数设置上与二维反卷积相似。